数据结构 - 树
2025年3月25日
目录
目录
树
完全二叉树
基本性质
完全二叉树有n个结点。
完全二叉树的深度 d=log2(n+1)
存储结构
主要存储方式:顺序存储+链式存储
顺序存储
各个结点的索引与顺序表位置一一对应,让结点的数据存放在顺序表相应位置的单元中。
顺序存储当数组,不过要开数组,可能实现空间浪费。

链式存储

有二叉链表和三叉链表,本质上就是有left,right,甚至还有一个parent的数据结点,指向上一个这个结点的父结点。

void createBinarytree(int value,node* left_tree,node* right_tree){
node *tree=new BinaryTreeNode();
tree.data()=value;
tree.left_tree()=left_tree;
tree.right_tree()=right_tree;//创建新的二叉树
}遍历概念
分为前序遍历,中序遍历,后序遍历
方法不同,本质是递归方式中访问根节点的时机不同。
先遍历左子树,再遍历右子树,访问根节点root是插入其中的。遍历时间是O(n)。

主要是中序遍历不太好理解。把A的左侧先遍历了,然后回到A,继续回到右侧遍历,但是FKC这里不好理解。
先遍历B的左子树D,对于D也是中序遍历的规则,先把D的左子树遍历了,对于D的左子树只有一个结点H,所以我们一开始就是H,然后遍历D的右子树I,然后回到D,来到B,接着遍历B的右子树E,由于E没有左子树,所以直接从空回到E,然后读取右结点,读取J,读完后B的整个左子树读取完成,接着我们回到A,然后读取C这颗右子树,由于C这棵树有左结点,所以我们读取F这颗左树,这棵F树的左结点为空,所以从空返回F,接着读取F的右树k,之后F这颗左树完全完成,回到C,C的右子树为空,所以此时此刻遍历结束。
话太多。
中序遍历就是:先读左边的小三角形 → 然后到顶点 → 最后读右边的小三角形。
注意,所有的结点遍历此时此刻都要遵循其递归算法的规则,所有节点,必须都是左数-右数,读取根结点的步骤插入其中,形成一种递归调用。从底部三角形模式读取。

通过计算二叉树的高度,可用后序遍历左子树+右子树,得到两个高度的最高作为树的高度。
表达式树
前缀和后缀和中缀读取。

本质上是栈+递归的读取。
遍历的非递归算法
也有非递归的转化算法,本质还是利用递归的本质,栈。
//前序遍历
void preorder(TreeNode* root) {
if (!root) return;
stack<TreeNode*> s;
s.push(root);
while (!s.empty()) {
TreeNode* node = s.top();
s.pop();
cout << node->val << " "; // 访问当前节点
if (node->right) s.push(node->right); // 先压右
if (node->left) s.push(node->left); // 再压左,保证左子树先出来
}
}
//中序遍历
void inorder(TreeNode* root) {
stack<TreeNode*> s;
TreeNode* curr = root;
while (curr || !s.empty()) {
while (curr) { // 先把左子树压栈
s.push(curr);
curr = curr->left;
}
curr = s.top();
s.pop();
cout << curr->val << " "; // 访问当前节点
curr = curr->right; // 转向右子树
}
}
//后序遍历
void postorder(TreeNode* root) {
if (!root) return;
stack<TreeNode*> s1, s2;
s1.push(root);
while (!s1.empty()) {
TreeNode* node = s1.top();
s1.pop();
s2.push(node); // 先压入第二个栈
if (node->left) s1.push(node->left); // 先压左
if (node->right) s1.push(node->right); // 后压右
}
while (!s2.empty()) {
cout << s2.top()->val << " "; // 访问顺序就是 左 → 右 → 根
s2.pop();
}
}//利用
也可以考虑队列来写。
void levelOrder(TreeNode* root) {
if (!root) return;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* node = q.front();
q.pop();
cout << node->val << " "; // 访问当前节点
if (node->left) q.push(node->left); // 先入左子节点
if (node->right) q.push(node->right); // 再入右子节点
}
}
//队列queue用于层序遍历二叉树的序列化与反序列化
序列化:遍历,得到结点的线性序列,转化成线性结构用于线性表的存储。
反序列化:根据线性序列重构原始的二叉树。
往往
前者基于遍历算法,后者依然得用栈来还原。
经典问题:用前序遍历和中序遍历结果重构二叉树,分析重构条件和算法的时间复杂度。
知道两个遍历,得到真正的二叉树结果。
前序遍历序列化&反序列化
都利用了递归来还原,将字符串与数据的互相转化。
基于前序遍历。
//序列化
void serialize(TreeNode* root, string& s) {
if (!root) {
s += "#,";
return;
}
s += root->val + ","; // 访问根
serialize(root->left, s); // 递归左子树
serialize(root->right, s); // 递归右子树
}
//反序列化
TreeNode* deserialize(istringstream& ss) {
string val;
getline(ss, val, ',');
if (val == "#") return nullptr; // 空节点
TreeNode* node = new TreeNode(val);
node->left = deserialize(ss);
node->right = deserialize(ss);
return node;
}层序遍历序列化&反序列化
利用队列queue。
string serialize(TreeNode* root) {
if (!root) return "#";
queue<TreeNode*> q;
q.push(root);
string res = "";
while (!q.empty()) {
TreeNode* node = q.front();
q.pop();
if (node) {
res += node->val + ",";
q.push(node->left);
q.push(node->right);
} else {
res += "#,";
}
}
return res;
}
//反序列化
TreeNode* deserialize(string data) {
if (data == "#") return nullptr;
istringstream ss(data);
string val;
getline(ss, val, ',');
TreeNode* root = new TreeNode(val);
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* node = q.front();
q.pop();
if (getline(ss, val, ',')) {
if (val != "#") {
node->left = new TreeNode(val);
q.push(node->left);
}
}
if (getline(ss, val, ',')) {
if (val != "#") {
node->right = new TreeNode(val);
q.push(node->right);
}
}
}
return root;
}最优二叉树(哈夫曼树)
带权二叉树
每个结点带有一个权重值。

带权路径长度
WPL=w1l1+w2l2+…+wnln
带权路径长度最小的二叉树,成为最优二叉树,即哈夫曼树。

基本性质
定理1:最优二叉树一定是满二叉树。
定理2: 最优二叉树中,如果两个叶结点的权重值不同,则权重值小的叶结点中的树的层数,大于等于权重值大的叶节点。
哈夫曼算法
一个至下而上的构建最优二叉树的方法,通过不断合并两个带权二叉树,最终生成最优二叉树。

构建哈夫曼树
时间复杂度:O(n^2)
//创建哈夫曼树代码
struct Node {
char ch; // 字符
int freq; // 频率(权值)
Node *left, *right;
// 构造函数
Node(char c, int f) : ch(c), freq(f), left(nullptr), right(nullptr) {}
};
// 自定义比较函数(优先队列默认大根堆,我们需要小根堆)
struct Compare {
bool operator()(Node* a, Node* b) {
return a->freq > b->freq; // 频率小的优先
}
};
// 构造哈夫曼树
Node* buildHuffmanTree(vector<pair<char, int>> freqList) {
priority_queue<Node*, vector<Node*>, Compare> pq;
// 初始化优先队列(最小堆)
for (auto& it : freqList) {
pq.push(new Node(it.first, it.second));
}
// 构建哈夫曼树
while (pq.size() > 1) {
Node* left = pq.top(); pq.pop();
Node* right = pq.top(); pq.pop();
// 创建新节点(合并两个最小节点)
Node* parent = new Node('\0', left->freq + right->freq);
parent->left = left;
parent->right = right;
// 插入新节点到优先队列
pq.push(parent);
}
// 最终根节点就是哈夫曼树的根
return pq.top();
}
哈夫曼树应用
哈夫曼编码
将文本字符串转化为二进制字符串编码。
在一般方案里,我们使用定长码,规定ascll码中的每个字符的编号。但我们这样的话空间花销大。所以我们可以使用不定长码来提高效率。
不定长码
使用频率高的字符采用短编码,频率低的字符采用长编码。
前缀码
一种常用的不定长码,每个字母的编码都不是其他字母编码的前缀。
(这样的编码可以避免读取的歧义,比如1101,可以看作1 101,也可以看作11 01,这样的歧义需要避免。)
构造示例:

其实还是很有意思的。我们可以算编码长度的加权平均数,即平均码长。
P为出现频率,W为码长。
树表示法
父指针表示法
保存父节点的索引。

一般用于实现并查集,时间复杂度为O(H),H为树的高度。
孩子表示法
存储的是结点所有的孩子,是一个子节点链表,存储的是头指针。
各个子节点按从左向右的顺序排列。

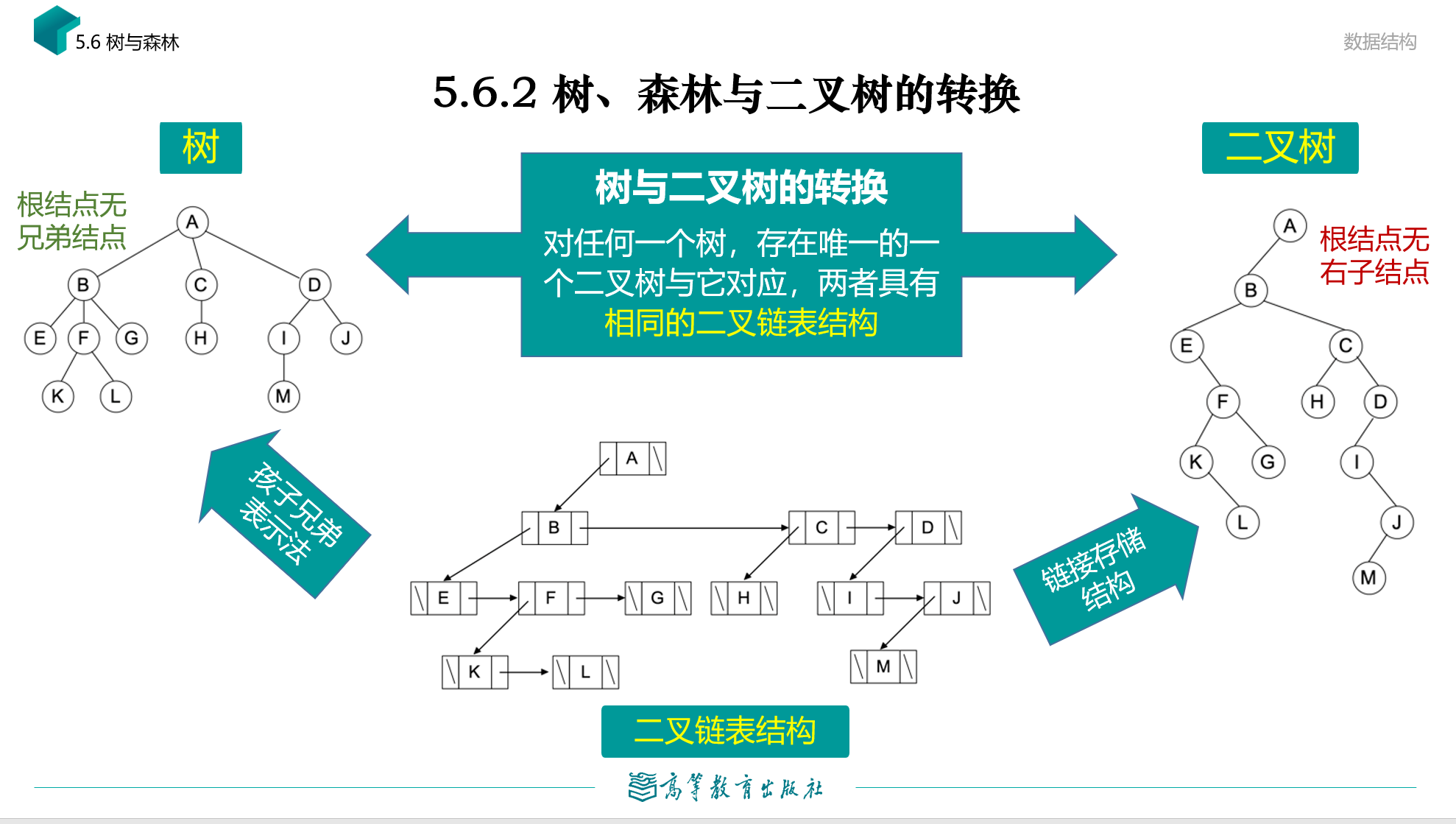
孩子兄弟表示法
常常使用二叉链表实现。每个节点存放它的第一个孩子和它的下一个兄弟的信息。
其实这个是最直观表现树结构的,兄弟信息代表所在层,孩子信息指向下一层。

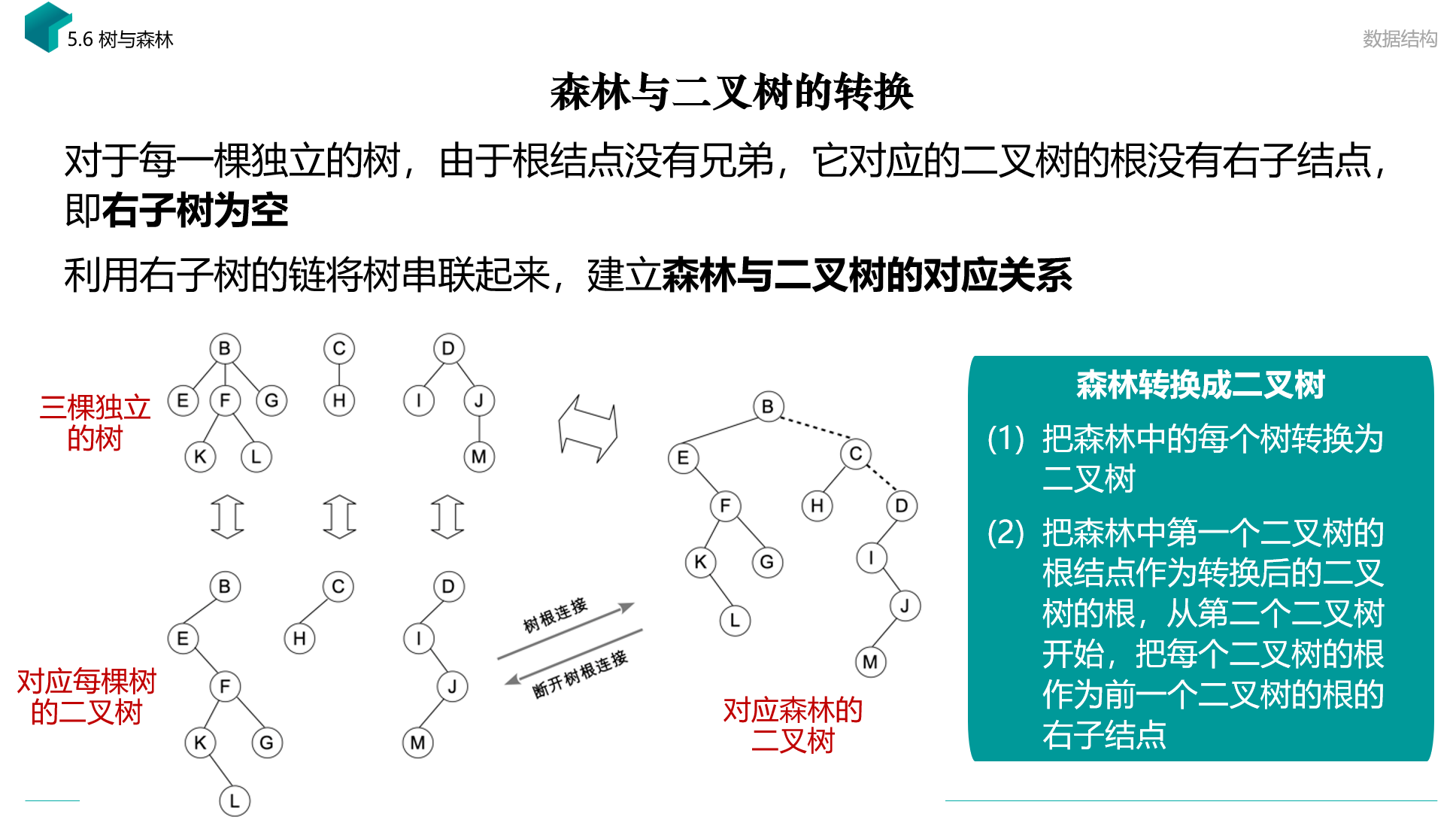
树与二叉树与森林的转换
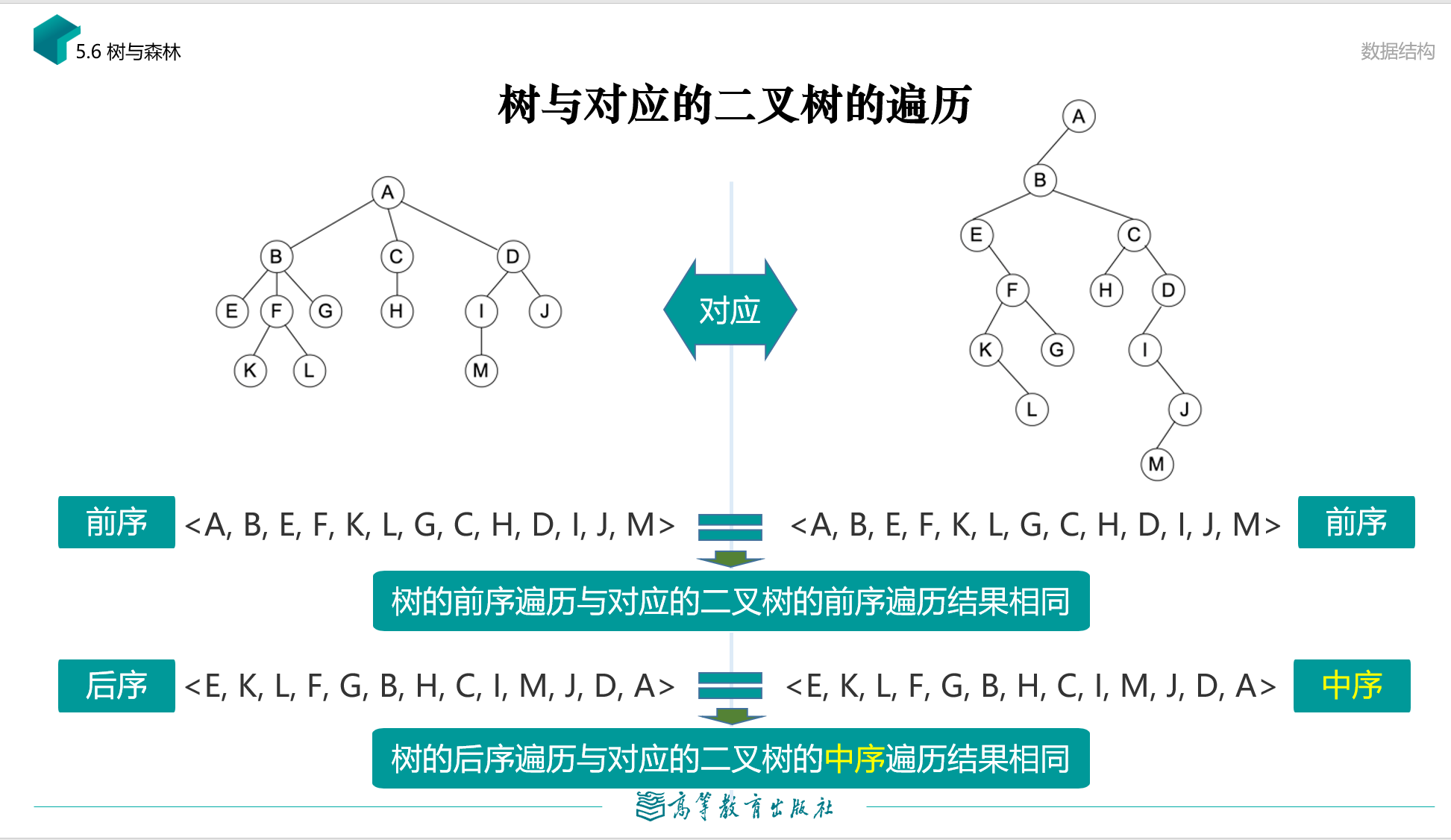
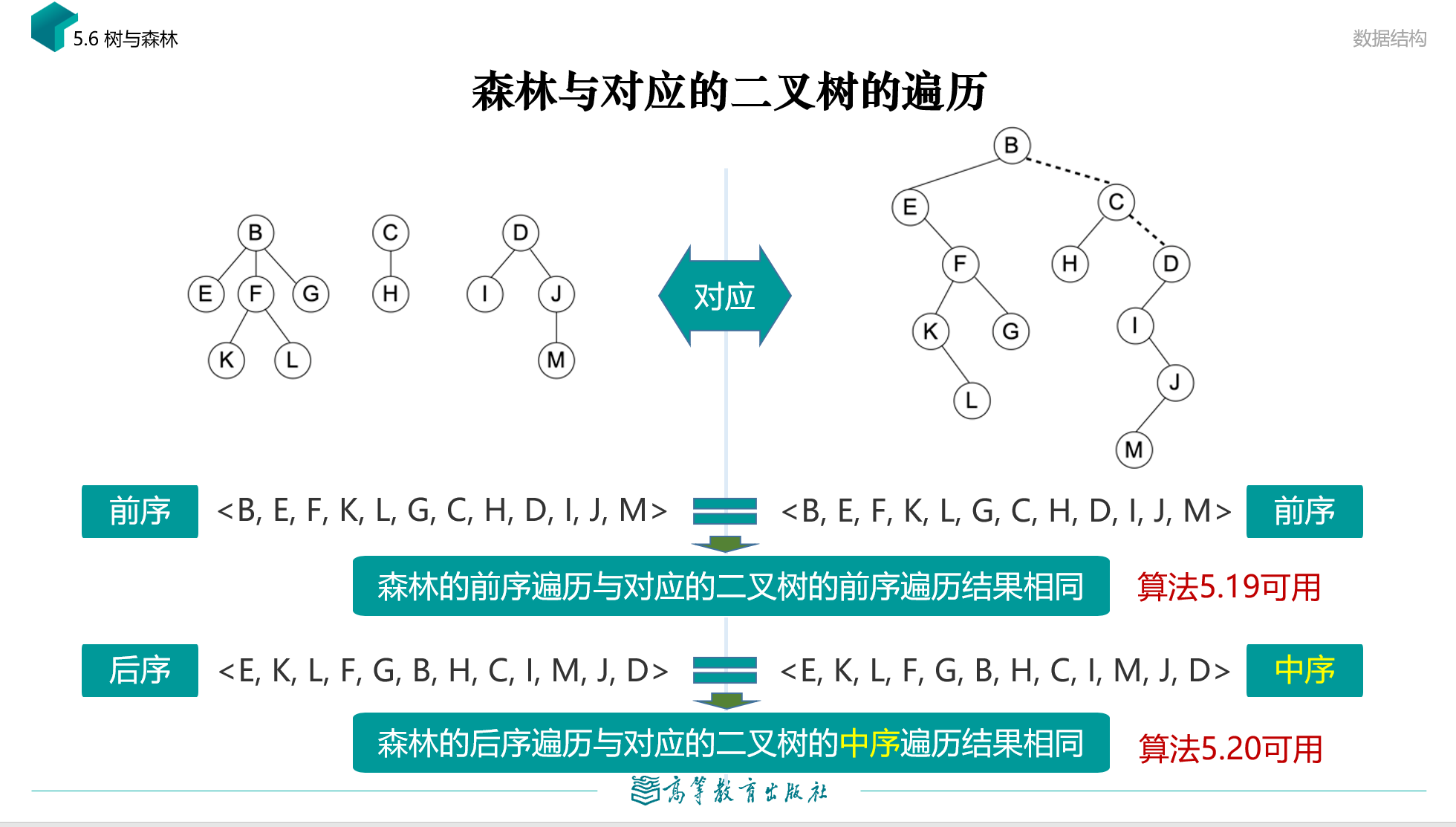
树和森林的遍历
树和森林的遍历都只有前序遍历和后序遍历,无中序遍历。
规则相同,都是从左到右,依次遍历。
树和森林的前序遍历与二叉树的前序遍历相同,后序遍历与二叉树的中序遍历相同,遍历时间复杂度与二叉树一样,都是O(n)。