数据结构 - 图

2025年4月8日

目录
目录

数据结构-图

图就是一群点与点之间的连接关系。

图 = 点 + 关系

我们一般利用矩阵对它进行计算。

图的术语

图的术语很多很多，分类记忆优先。

一类：必须掌握，写代码会直接用到的术语

这些术语不仅是定义，更是写代码、分析题目的关键词

术语意义
有向图 / 无向图箭头 vs 无箭头，影响建边方式（add(u,v) 是否对称）
邻接（Adjacency）一个点相邻的所有点，用于 DFS / BFS
出度 / 入度 / 度出去多少条边、进来多少条边，图遍历/拓扑排序常用
加权图边有权值了，要用 edge.to, edge.w 来写
简单路径 / 简单环不重复点的路径 / 环，DFS 搜索路径时要判断
子图原图的一部分，图论算法经常讲“找子图”

二类：理解了就能用的术语

这些术语不是写代码的前提，但出现在算法分析里，比如题干说“强连通分量”，得知道那是啥

术语建议
连通图 / 强连通图DFS/BFS 一遍能走完 vs 每个点都能互相到达
连通分量 / 强连通分量把图分成“互相能到达的块”
极大连通子图不能再扩展的连通分量，Tarjan算法中会用
网络（flow network）用于网络流，前期接触少，可以见到再查
回路 / 环 / 简单环DFS 检测环判断用，图论题会提到

画成图理解，有题再回笔记复习，不需要死记硬背术语。 让G老师整理了一个简略的模板，复制粘贴一下。

图论术语学习笔记，仅供查阅

术语中文解释图论举例代码意义 / 使用场景
有向图边有方向，A→B 与 B→A 不同A → B → C邻接表只存 u→v，不加反边
无向图边无方向，A-B 是双向的A - B - C建边要加两次 u↔v
邻接某个点能直接到达的点A 相邻点为 B, CDFS / BFS / 最短路核心
入度进入该点的边数C 有入度 2：A→C, B→C拓扑排序判断是否入度为 0
出度从该点出发的边数A 有出度 1：A→B构建邻接表或最短路用
度无向图中与该点相连的总边数B 有度 3：连了 A, C, D统计图结构复杂度
加权图每条边有权重值（如距离、代价）边 A→B 权重为 3需要额外记录权重 edge.w
简单路径路径中点不重复A→B→C 合法DFS 中用 visited[] 防止重复
简单环 / 回路点不重复的闭环A→B→A 是简单环判断是否有环
子图图的一部分（点与边的子集）G 的子图仅含 A, B, C大图中划分子问题
连通图任意两个点之间有路径一笔能走完所有点用 DFS / BFS 判断连通性
强连通图有向图中任意两点互达所有点之间都有双向路径Tarjan 算法中强连通分量（SCC）判定
连通分量连通图中独立的“块”一个图被分成多个连通子图并查集找连通块 / 统计图中有几个分量
强连通分量强连通图中的“极大块”Tarjan 算法识别强连通部分拆图结构、题目要求找 SCC 时使用
极大连通子图无法再扩展的连通图一次 DFS 得到的整块判最大图结构 / DFS 局部图遍历
极小连通子图包含所有点、最少边的连通图，去掉一条边就不连通，增加一条边就成环原图有环，生成树去掉了冗余边用来描述 MST 的性质/写题时判断图是否成树常用
网络（flow）带容量限制的有向图边 A→B 最大流 5最大流 / 最小割等网络流建模

比较

线性、树、图结构中

实现

ADT的C++类表示

Graph 是一个支持添加边、遍历（DFS/BFS）、获取邻接点的抽象图结构。
支持有向图和无向图的建图形式，底层使用邻接表实现。适合作为图论算法的基础类。

// 图的抽象数据类型（ADT）结构表示
class Graph {
private:
    int V; // 顶点数量
    bool directed; // 是否为有向图
    vector<vector<int>> adj; // 邻接表表示图

public:
    // 构造函数：初始化图的顶点数量与有向/无向标志
    Graph(int vertices, bool isDirected = false) {
        V = vertices;
        directed = isDirected;
        adj.resize(V);
    }

    // 添加一条边（u 到 v）
    void addEdge(int u, int v) {
        adj[u].push_back(v);
        if (!directed) {
            adj[v].push_back(u); // 无向图加双向边
        }
    }

    // 获取一个点的所有邻接点
    vector<int> getNeighbors(int u) {
        return adj[u];
    }

    // 深度优先遍历（DFS）
    void DFS(int start, vector<bool>& visited) {
        visited[start] = true;
        for (int v : adj[start]) {
            if (!visited[v]) {
                DFS(v, visited);
            }
        }
    }

    // 广度优先遍历（BFS）
    void BFS(int start) {
        vector<bool> visited(V, false);
        queue<int> q;
        q.push(start);
        visited[start] = true;
        while (!q.empty()) {
            int u = q.front(); q.pop();
            for (int v : adj[u]) {
                if (!visited[v]) {
                    visited[v] = true;
                    q.push(v);
                }
            }
        }
    }

    // 获取图中顶点数量
    int getVertexCount() const {
        return V;
    }

    // 获取图中某点的度数（无向图）或出度（有向图）
    int getDegree(int u) const {
        return adj[u].size();
    }
};

存储

图的存储用于存储点和边的关系，主要有2种方法。

邻接矩阵（二维数组）

对于稠密图，有向图，采用邻接矩阵非常合适。但存储大量无边信息，造成空间浪费。 这个很好构造，创一个二维数组，赋值关系间就好。比如1号元素指向2号元素，权值为2，则 g[1][2]=2 对于一些有权图问题，我们为了代码能跑，经常会设置INF，辅助最小路径问题，这样输入也方便

if (graph[i][j] == 0 && i != j) graph[i][j] = INF;

邻接表

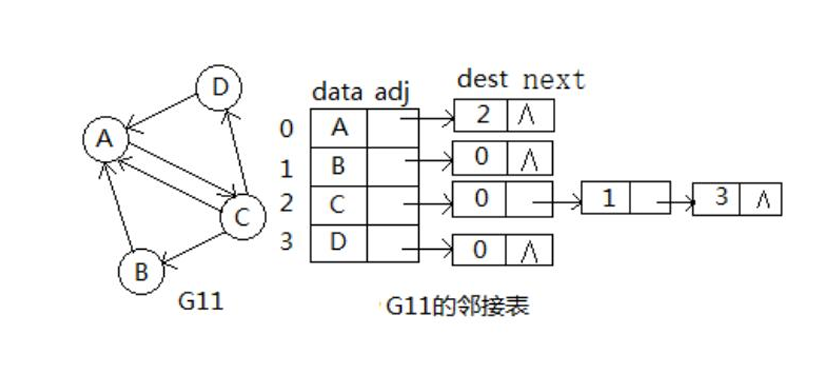
邻接表的实现和邻接矩阵很像，但不约束于邻接矩阵n*n的固定大小。 每一个顶点使用一个一维数组来存储，而边的存储是同一个顶点出发的所有边，组成一条单链表。 我们用 STL 实现的话，vector 的 push_back() 很好的起到了邻接表的实现来存储图。邻接表就是链表式的图结构。 当然也可以直接用链表，跳转。 对于稀疏图，无向图，采用邻接表非常合适。空间利用效率大幅度提高，不存储无边的无用信息。

STL 实现

无权图版本

//基本结构
const int N = 10010; // 最大点数
vector<int> graph[N]; // 邻接表：graph[u] 存放 u 的邻接点

//加边操作
void addEdge(int u, int v) {
    graph[u].push_back(v);
    graph[v].push_back(u); // 无向图要加两次
}

//遍历
for (int v : graph[u]) {
    // u → v 有一条边
}
//非常类似链表遍历，每个点自己的链表就是vector

有权图版本

vector<pair<int, int>> graph[N]; // pair<to, weight>

void addEdge(int u, int v, int w) {
    graph[u].push_back({v, w});
    // 如果是无向图：
    // graph[v].push_back({u, w});
}

for (auto [v, w] : graph[u]) {
    // u → v, 权重为 w
}
链表实现
struct Graph {
   struct Node {//边的构造
       int to;           // 边通往哪个点
       Node* next;       // 还有没有其他边从该店出去
   };

   Node* head[N];        // 图的点对应的边，是数组
};

void addEdge(int from, int to) {
   Node* newNode = new Node{to, head[from]};
   head[from] = newNode;
}
//插入边

“如果一个点有很多出边怎么办？如果没有出边怎么办？”

那我们就反向思维，我们链表存储的是图的边，并非图的所有点。点可以对应很多边，但边可以对应只有两个点。而且我们图的关系，看的往往是边的关系。

插入边直接 addEdge(1,2)，插入一条从1指向2的边。我们每一次构造都是插入 Node 。 head[from] = newNode 表面上是赋值，
但这行代码背后的意义是：

把新的边插在原链表的最前面，原来的边通过 newNode->next 继续挂在后面。

建立新节点的时候 new node{to,head[from]} 把旧的链表接在新边后面，实现了“头插法”追加”。

遍历

遍历图和遍历二叉树不太一样，图的每个顶点地位相同，我们要判断“一个点是否被访问过”，避免遗漏。

DFS

其实感觉有点像开 bool 数组呢… 深度优先遍历。 访问方式：

从指定点开始深度优先遍历，我们先把一个点变成 true ，从它开始…

void DFS(Graph G, int v, bool visited[]) {
    visited[v] = true;         // 标记当前点已访问
    for (每一个与 v 相邻的顶点 u) {
        if (!visited[u]) {
            DFS(G, u, visited);  // 递归访问未访问的邻居
        }
    }
}

BFS

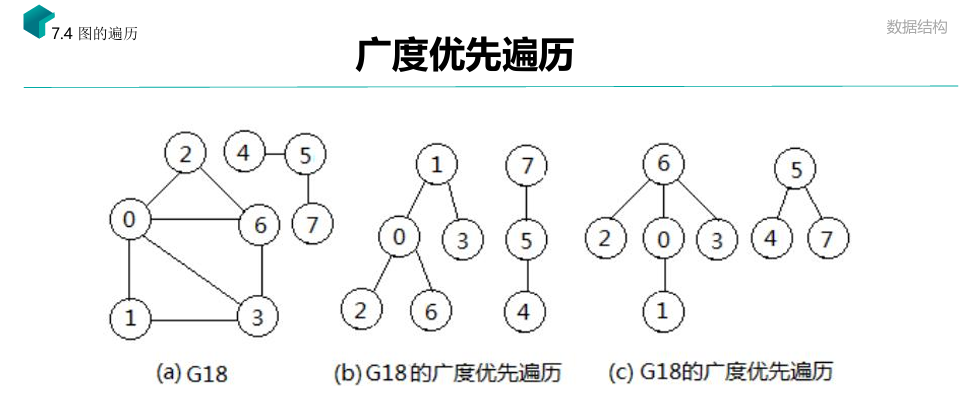
广度优先遍历。 访问方式：

与深度优先不太一样的是，广度优先像是 “访问邻居“，确保从一个点出发，所有与该点连接的点都遍历到，然后再跳转下一点。

注意：

void BFS(Graph G, int start, bool visited[]) {
    queue<int> q;
    visited[start] = true;
    q.push(start);  // 起点入队

    while (!q.empty()) {
        int v = q.front(); q.pop();   // 取出当前点
        for (每一个与 v 相邻的顶点 u) {
            if (!visited[u]) {
                visited[u] = true;    // 标记为已访问
                q.push(u);            // 邻居入队
            }
        }
    }
}

应用

最短路径问题（Dijkstra，Bellman-Ford，Floyd-Warshall）

定义：在最短路径问题中，给定一个带有权值的有向图 G=(V,E)，令w(u,v)表示边(u,v)的权值。图中一条路径p=<v_0,v_1,…,v_k>的权值w(p)是构成该路径的所有边的权值之和，在所有的从顶点u到顶点v的路径当中，权值最小的那条路径称之为从u到v的最短路径。 说白了就是每次都走权值最大or最小的路径。最后整条路径是权值最大or最小的。

重要性质：给定两个顶点之间的一条最短路径，则在该路径上任意两个点的路径都是最短的，这种最短子路径称为最优子结构。 一条大路是最优解，那么每条小路都是最优解。

我们用动态规划，Dijkstra算法的基础，就是基于这个“每条小路最优解”。

问题： 一条最短路径能包含环路吗？

答：不能。绝不行。不管环的权值是负的、正的，还是零，全都不行。

如果环的权值是负数 (这玩意最危险）

假设你从 A 出发，走到某个地方遇到了一个负权环，也就是说，这个环越绕越“省钱”。 那干嘛不在这个环里绕一百万圈，搞个负无穷大？你这什么最短路径，明明还可以更短！ 只要图里能从起点走到一个负权环，那你永远也找不到真正的最短路径， 结论：负权环 = 最短路径永远没完没了。

如果环的权值是正数（这玩意没啥用）

你走了一条路，中间绕了个小贵环回来，然后再继续走。
那你为啥要走那个贵环？你删掉它不是省更多？ 只要路径里有正权环，你都可以删掉它，剩下的路更短。 结论：正权环 = 拖后腿，没必要。

如果环的权值是 0（ 这玩意最容易骗你）

你以为走这个 0 环“也没多付钱啊”，那可太天真了。
虽然它不会让路径更差，但它也不会让路径更好，
而且它让你走了一圈纯属浪费感情。 结论：0 权环 = 没损失但也没价值，是废环，删了也不影响最短路径。

Dijkstra算法

手写作业写最短路径的时候，按教材那个表达来。 遍历+贪心。 流程：

实例： 题目 顺便给一下教材写法，考试格式… image.png

终点i=1i=2i=3i=4i=5
1⟨4,1⟩20⟨4,2,1⟩15⬛ ⟨4,6,1⟩12
2⬛ ⟨4,2⟩5
3⬛ ⟨4,2,3⟩8
5⬛ ⟨4,5⟩11⟨4,2,3,5⟩23(舍)⟨4,6,5⟩13
6⬛ ⟨4,6⟩10
u(选好的最短路径节点)23651
s(已确定最短路径的节点集合){4,2}{4,2,3}{4,2,3,6}{4,2,3,6,5}{4,2,3,6,5,1}
最终结果（最短路径）：

代码实现（这里是把所有点到点的距离全部计入了）：

void dijkstra(int n, int start, vector<vector<int>>& graph) {
    vector<int> dist(n, INF);     // 存储起点到各点的最短距离
    vector<bool> visited(n, false); // 标记哪些点已经确定最短路径

    dist[start] = 0; // 起点到自己的距离是0

    for (int i = 0; i < n; i++) {
        int u = -1;
        int minDist = INF;

        // 找当前未访问的点中，距离起点最近的那个
        for (int j = 0; j < n; j++) {
            if (!visited[j] && dist[j] < minDist) {
                u = j;
                minDist = dist[j];
            }
        }

        if (u == -1) break; // 如果没找到说明剩下的都不可达，结束

        visited[u] = true; // 标记这个点已经确定最短路径

        // 更新与u相邻的点的距离
        for (int v = 0; v < n; v++) {
            if (!visited[v] && graph[u][v] != INF) {
                if (dist[u] + graph[u][v] < dist[v]) {
                    dist[v] = dist[u] + graph[u][v];
                }
            }
        }
    }

    // 输出结果
    for (int i = 0; i < n; i++) {
        if (dist[i] == INF)
            cout << "从" << start << "到" << i << "：不可达" << endl;
        else
            cout << "从" << start << "到" << i << "：最短距离 = " << dist[i] << endl;
    }
}

Bellman-Ford算法

核心思想：Bellman-Ford算法通过对边进行松弛的方式渐近地求出源顶点s到其余顶点v的最短路径距离。

Bellman-Ford 的核心机制就是： “你别急，我帮你把路径松弛 V-1 次。” 啥叫“松弛”？不是拉筋，是更新路径：

每次松弛，就是尝试：

“如果从 A 到 B 这条边能让 B 的最短距离更小，我就更新一下到达 B 的最短距离。”

你把图里所有边一遍一遍扫，
每发现能更新的路径，就更新。
重复这个过程 V-1 次（V = 点的数量）。

因为最短路径最多经过 V-1 条边，
再多就是环了，你就绕圈圈了。

“如果我松弛了 V-1 次还没完，
第 V 次还能继续更新，那说明你有 负权环，无限省钱大骗局，整个图炸了。”

代码实现：

bool bellmanFord(int n, int start, vector<Edge>& edges, vector<int>& dist) {
    dist.assign(n, INF);
    dist[start] = 0;

    // 进行 n-1 次松弛操作
    for (int i = 0; i < n - 1; i++) {
        for (auto edge : edges) {
            if (dist[edge.u] != INF && dist[edge.u] + edge.w < dist[edge.v]) {
                dist[edge.v] = dist[edge.u] + edge.w;
            }
        }
    }

    // 第n次松弛，检测是否还有可以更新的——有就代表存在负权回路
    for (auto edge : edges) {
        if (dist[edge.u] != INF && dist[edge.u] + edge.w < dist[edge.v]) {
            return false; // 有负权环
        }
    }

    return true; // 成功，没有负权环
}

有负权环没答案。答案存在 dist 数组里。

Floyd-Warshall算法

算法介绍：Floyd-Warshall算法是一种动态规划算法，能解决所有顶点对最短路径问题，运行时间为O(|V|^3)，能够处理权值为负的边。 代码更短。

核心思想：如果你想让 i 到 j 更短，那试试看从 i 到 k 再到 j 会不会更便宜。

你有一张图，任意两点之间的最短路径你都想知道，一个一个试太累，那你干脆：
让每个点都轮流当“中转站”，看看是不是能让两点之间的距离变短。

本质： 你要更新的路径是 dist[i][j]，
每当你发现： dist[i][j] > dist[i][k] + dist[k][j]

你就做一次松弛 dist[i][j] = dist[i][k] + dist[k][j];

代码不太优雅： 从 i 到 j，如果我中转一下 k，是不是更便宜？

for (int k = 1; k <= n; ++k)  // 中转点
    for (int i = 1; i <= n; ++i)    // 起点
        for (int j = 1; j <= n; ++j)// 终点
            if (dist[i][j] > dist[i][k] + dist[k][j])
                dist[i][j] = dist[i][k] + dist[k][j];

不能有负环，否则结果会出事（无限套现）。

最小生成树（最小支撑树）问题（生成MST）

定义：给定一个连通的加权图G=(V,E)，其中V为顶点的集合，E为边的集合，其中E中的每条边都有一个非负的权值。最小生成树问题是在G中求解权值最小的生成树（MST）。

Prim算法

是一个贪心算法，构造树的时候，每次都是选择权值最小的路径连接点与点。 一个点出发，慢慢往外连边，每次都选：

“从已经连接好的点，到外面去的边中，最短的那一条。”

prim算法和Dijkstra算法的思想很像很像，不过一个是关注单纯点到点的路径的权值，一个是关注从源点到该点的路径和。也要注意保留未选取路径中指向未选取点的。

照样不能去成环，理由和最短路径的那个一样的。

代码实现：
#include <iostream>
#include <vector>
#include <climits>

using namespace std;

const int INF = INT_MAX;
const int N = 100; // 最大顶点数

int graph[N][N]; // 邻接矩阵
vector<bool>visited(N,false); // 标记是否加入MST，哪些点已经被我们选了
vector<int>dist(N,INF)     // 到MST的最小边权值，初始每个点都贵得离谱
int n;           // 顶点数量

int prim(int start) {

    dist[start] = 0;
    int totalWeight = 0;

    for (int i = 0; i < n; i++) { 
    //给每一个点找最便宜的权值,处理后加上去
        int u = -1, minDist = INF;
        //从还没选的点中选一个最便宜的
        for (int j = 0; j < n; j++) {
            if (!visited[j] && dist[j] < minDist) {
                minDist = dist[j];
                u = j;
            }
        }

        if (u == -1) break; // 找不到了，说明不连通

        visited[u] = true; // 找到了，标记一下，下次不选它了，不然有可能形成环路
        totalWeight += dist[u]; // 加一下找到的u点出发最短权值

        // 更新从点 u 出发可以到达的，但还没去过的其他点的，权值，便于下次选择最短路径
        for (int v = 0; v < n; v++) {
            if (!visited[v] && graph[u][v] < dist[v]) { 
	        //v 点我还没去过，并且我发现u到v点的路径比我一开始设定的minDist还要短，那我就把它改成u到v的边，调整一下
                dist[v] = graph[u][v];
            }
        }
    }

    return totalWeight; // 输出最短路径
}

int n;
cin >> n;
vector<vector<int>> graph(n, vector<int>(n));

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        cin >> graph[i][j];
        if (graph[i][j] == 0 && i != j) graph[i][j] = INT_MAX; // 无边当作 ∞
    }
}

Prim 算法遍历邻接矩阵所有点，平均时间复杂度为O(n^2)。

 #include <iostream>
#include <vector>
#include <queue>
using namespace std;

struct Edge {
    int to, weight;
    bool operator>(const Edge &e) const {
        return weight > e.weight;  // 小根堆
    }
};

const int N = 1001; //顶点最大个数
vector<Edge> graph[N]; //图，邻接表表示的，数组索引i表示是第i个节点，存的是边链表的头
bool visited[N];

int prim(int start) {
    priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
    visited[start] = true;

    for (auto &e : graph[start]) pq.push(e); 
    
    int total_weight = 0;

    while (!pq.empty()) {
        Edge curr = pq.top(); pq.pop();
        if (visited[curr.to]) continue;

        visited[curr.to] = true;
        total_weight += curr.weight;

        for (auto &e : graph[curr.to]) {
            if (!visited[e.to]) pq.push(e);
        }
    }
    return total_weight;
}

Kruskal 算法

算法思想很简单：

我先把全世界最便宜的边找出来，想加就加，只要它不会成环。

那么先把边按权值大小排序，从上往下加入边，如果不成环就加。（这里判断是否成环需要用到并查集）。 代码之后补充，因为还没了解并查集😿。

拓扑排序算法

image.png

拓扑排序还是很容易去理解的，我们根据前后关联性可以轻松写出它的拓扑排序。 拓扑排序算法一般还是用于查找该图“是否有拓扑排序”。

关键路径

从起点到某点的最长路径称为起点到该点的关键路径。一般用于AOE网络。 image.png

关键路径上的活动被称为关键活动。 对于一个图的优先调度，有多余的人力物力放在非关键路径上其实是不起效果的。 求解关键路径： image.png

目标：从 v₀ 出发走到 v₈，找出耗时最长但不能耽误任何环节的一条路径，也就是“关键路径”。

A. 先算每个事件的 earliest[v] 从起点 v₀ 开始，最早发生时间记为 0 然后向下游传播，按下式推：

earliest[v] = max{ earliest[u] + weight(u,v) }

按顺序来算：

于是你现在有了 earliest[v] ：见图中绿色数字。

B. 反过来算 latest[v]（从终点往前推） 从终点 v₈ 开始：

latest[u] = min{ latest[v] - weight(u,v) }

倒着来算

C. 计算每条活动的 e[i] 和 l[i] 对每条活动 aᵢ： e[i] = earliest[u] （活动起点的最早时间） l[i] = latest[v] - weight(u,v)（终点最晚时间-任务耗时） 若 e[i] == l[i]，说明该活动不能晚，就是关键路径的一部分！

我们来实际举几个： a₀（v₀→v₁）：

a₄（v₁→v₄）：

a₆（v₃→v₆）：

连接所有 e[i]=I[i] 的点，得到关键路径。 最终关键路径是：

v₀ → v₁ → v₄ → v₇ → v₈

总耗时：5 + 4 + 5 + 8 = 22（也就是项目最早完成时间）